BASIC

The winLIFE BASIC module covers the essential basics of analytical fatigue life prediction. Typically, winLIFE users start their work with this module. The following extensions are available for the BASIC module, which can be purchased additionally:

winLIFE MULTIAXIAL

winLIFE MULTIAXIAL MULTICORE

winLIFE GEARWHEEL&BEARING

winLIFE CRACKGROWTH

winLIFE VIEWER4WINLIFE

winLIFE RANDOM FATIGUE

winLIFE STATISTIC

winLIFE Project Management System

Typical industrial tasks involve not only a single analytical fatigue life prediction, but usually a large number of load cases and variants.

For this purpose, winLIFE offers a powerful project management system that can handle up to 2000 projects simultaneously. The picture below shows the user interface where 8 projects are defined. The projects can be edited individually, but they can also be started together and superimposed.

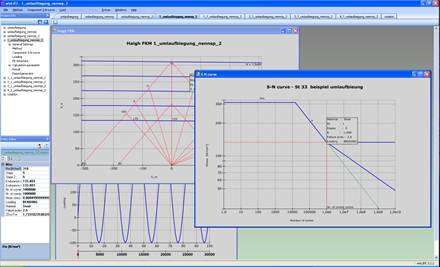
A project generator enables the generation of projects in which individual parameters can be systematically varied.

As many calculations lead to long computing times, an automated process is important, so that the possibility of batch processing is of great importance. The project files are saved in XML format and can also be started as a batch from the user interface.

How do I obtain Material Data for an Analytical Fatigue Life Prediction?

winLIFE offers several options for obtaining material data for the analytical fatigue life prediction. In addition to generation based on static material data, extensive material databases are included in the scope of delivery.

Generation of S-N Curves from Static Material Data

As winLIFE has many customers in the wind energy, shipbuilding and general engineering sectors, special input generators have been created to generate fatigue life data from static material parameters. These are

• S-N curve generator for welded joints according to Germanischer Lloyd for shipbuilding
• S-N curve generator for welded joints according to Germanischer Lloyd for wind turbines
• S-N curve generator for welded joints according to the FKM-guideline
• S-N curve generator according to Hück, Trainer, Schütz
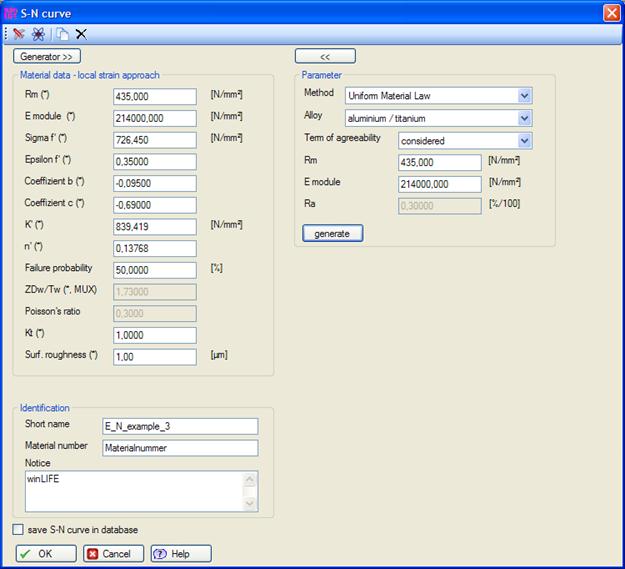
• Generator according to Uniform Material Law

The following figure shows an example of an input mask for a generator according to the FKM guideline, which is based on a wealth of experience and is already established in many areas. The S-N curve can be estimated from static material data such as yield strength, tensile strength and component information such as surface, notch factor, stress gradient, etc.

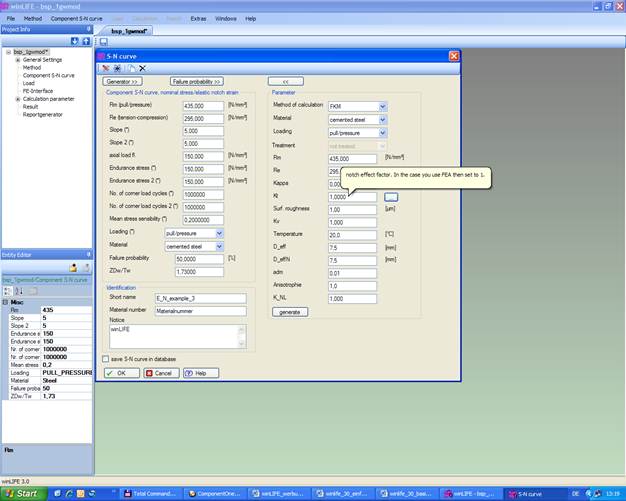
The figure above shows the input screen used to generate these S/N-curves. Once generated, the user can partially overwrite the data to modify known individual values.

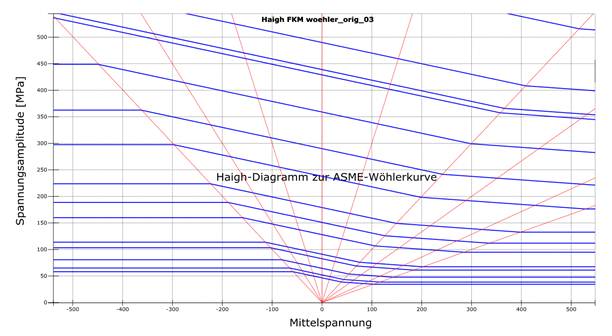
In addition to the S-N curve, the Haigh diagram is also used to provide more comprehensive information, as it also shows the mean stress sensitivity and the yield and break points (see next figure).

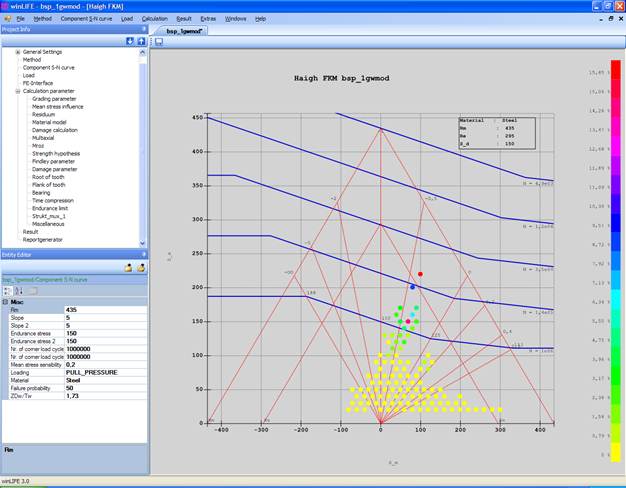
If the probability of failure is important to an investigation, any number of S-N curves with different probabilities of failure can be derived from the 50% S-N curve, taking into account different scatters in the range of fatigue strength for finite life and fatigue limit.

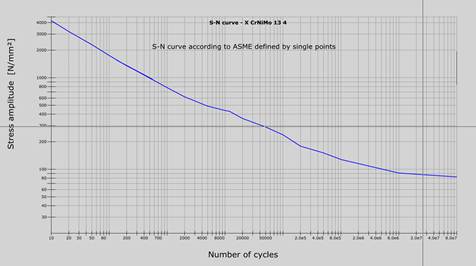
S-N Curves defined Point by Point (ASME CODE)

The S-N curve of a component is defined by a large number of individual points between which interpolation takes place. This definition of the S-N curve has now been implemented in winLIFE at the the customer's request. The following example shows such a S-N curve.

Generation of component S-N curves for welded components

Component S-N curves can be generated in accordance with the FKM, Germanischer Lloyd (shipbuilding, wind energy), IIW guidelines. Fatigue life can be calculated according to the nominal stress concept or the structural stress concept.

The geometry and notch factors are taken into account by assigning them to a catalogue of different weld seams (detail classes, FAT classes).

Powerful macros for FEMAP and ANSYS are available for data transfer to winLIFE.

GENERATION OF STRAIN S-N CURVES

Strain S-N curves can be generated from static material characteristics. In addition to the most commonly used Uniform Material Law, other algorithms are available.  The procedure is shown in the figure below: Static material characteristics are specified (right-hand side) and the material characteristics for the S-N curve and the cyclic behaviour are generated from them (left-hand side).

The following figure shows a calculation example where the cyclic data was obtained and displayed by generating it from the static characteristic values. The shape factor and surface roughness in the notch have been specified for the component. The stress-strain curve in the notch is calculated for the component from the rainflow matrix. The curve can also be calculated directly from the material memory without rainflow counting.

Material Databases

The following material databases are supplied with the installation:

Material database for the local concept
Material database according to FKM
User database

Material Database for the Local Strain Concept

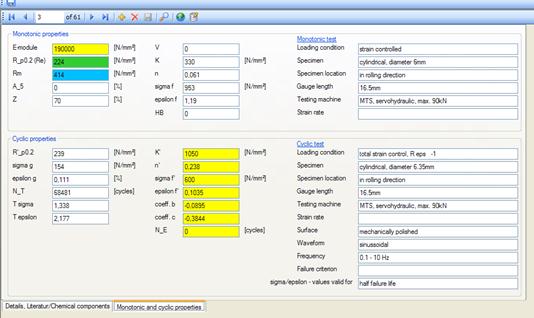
An extensive database (more than 1000 materials) with the following
information is available for calculations according to the local concept:

• Static material characteristics
• Cyclic material characteristics
• General information and, in particular, information sources

Own data can be integrated into the database.

Material Database for Calculation according to FKM

Common material data from trial tests can be taken from the supplied database with data from the FKM guideline.
This data can be used to generate S-N curves for the component.

By entering the component data in addition to the material data, a component S-N curve can be generated and stored in the user database.

User Database

The winLIFE user saves the material/component data used for the fatigue life calculation in a user database containing the material and component information.

Obtaining the Load Data

For a fatigue life calculation, data on the acting load is required. This can be a measured load-time curve or a frequency distribution of loads (load spectrum).

Definition of a Load Spectrum

A load spectrum is defined by the following triplet of values

• Mean load
• Load amplitude
• Number of cycles

Experience in various fields of engineering shows that the acting load spectra have certain basic forms that are easy to describe. If you know the basic form of the acting load spectra - e.g. from publications - you can easily generate a load spectrum adapted to the individual component with the winLIFE spectrum generator.  The following figure shows three such basic forms of load spectra generated with winLIFE.

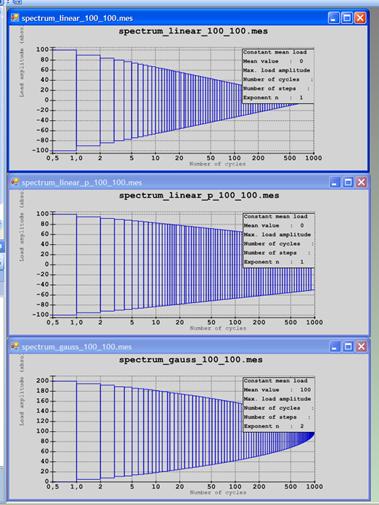
USING LOAD-TIME HISTORIES

Another way of describing loads is to use load-time histories. A load can be a stress, a torque or a force. Such data can be obtained from measurements, but it is also possible for the user to enter the load-time curve manually using the keyboard. Alternatively, the sine generator can be used to easily generate load-time functions.

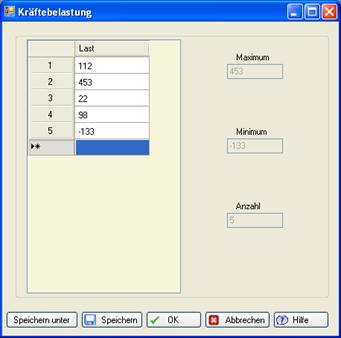
Loads (Manual Input)

Loads - e.g. forces as a function of time - are entered in the input screen and then saved. For time reasons, only short load sequences are entered in this way.

Force Generator (Sine Curve)

It is often required to generate simple load-time curves quickly and easily. This is possible with the sine curve generator described here.

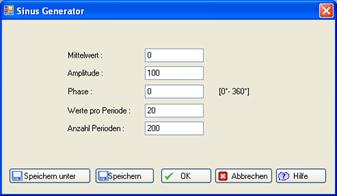
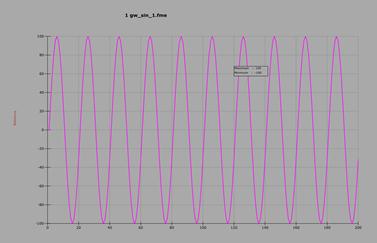
The entries should be self-explanatory. The result of the generation looks like this:

Import of Measured Load-Time Functions

In most cases, very large measurement data is used, which can be several gigabytes in size.

Interactive data post-processing in the graph allows easy correction of the load-time history or load spectrum data. For example, spikes can be quickly removed and corrections made to signal drift.

The rainflow matrix used by winLIFE can also be post-processed. The rainflow matrix contains the damage-relevant events and displays their degree of damage using a colour scale. By changing the rainflow matrix, alternative load scenarios can be easily simulated.

In the local concept, the stress-strain curve can be visualised. It is visualised from the rainflow matrix and the cyclic material characteristics.

ANALYSIS IN THE FREQUENCY RANGE

The natural frequencies of a dynamically excited system and the frequency spectrum of the excitation have a major influence on the fatigue life. It is therefore very useful to determine the stresses acting on a component using the Power Density Spectrum (PSD). Components are often tested on an oscillating table using this PSD of acceleration. winLIFE RANDOM does exactly this. The module is introduced in a separate chapter.

Using FEA

winLIFE can import data from FEA and use it for the fatigue calculation. In this case the local stresses and further conditions of each node are considered. 

Because, generally speaking, not all the nodes of a structure are endangered - the damage usually begins on the surface - the user can select nodes for the fatigue life calculation according to various criteria. By doing this, the number of nodes to be examined can be substantially reduced and the calculation time shortened accordingly. 

Macros are supplied with winLIFE so that data can be transferred from FEA-Programs.  The results from winLIFE, i.e. the damage for each individual node, can be shown by the FEA-program in colour.  A separate colour is used for each different range of damage.  The FEMAP user-interface is available for all data transactions between winLIFE and NASTRAN Users will therefore have no difficulties using this program.

winLIFE is used in collaboration with the following FEA-codes:

• FEMAP-based programs like MSC.NASTRAN, NEiNASTRAN and NX.NASTRAN, WTP2000
• IDEAS
• SAMCEF

The interface to FEA is described in detail and many users wrote their own interface. Successful links to MEDINA, ANSYS and other programs were achieved.

Short description of the calculation procedure for an example

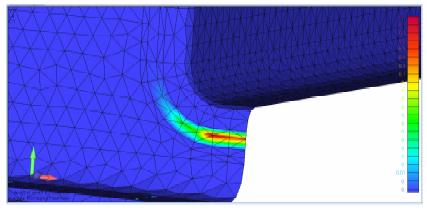
In a short description the fatigue calculation procedure is shown. The following figure shows a part of a truck suspension which is loaded dynamically by a force (see over next figure). Because of the symmetry only half of the part is analysed.

In the first step a static FEA calculation is used to ascertain the stress within the component.  For this purpose the state of stress is calculated in a structure which is subjected to a standard load Fo. The direction of the standard load must correspond to the acting force F(t).

The elastic stress for each load F(t) can then be calculated in a linear way corresponding to the quotients F(t)/Fo.  If, for example, a force F(t) exists as shown in the next figure, then the stress within a component can be calculated for any required moment. In the case of local concept, there is an actual stress-strain curve.  This means that the actual stress path for each node, including plastic deformation can be calculated using Neuber's rule.

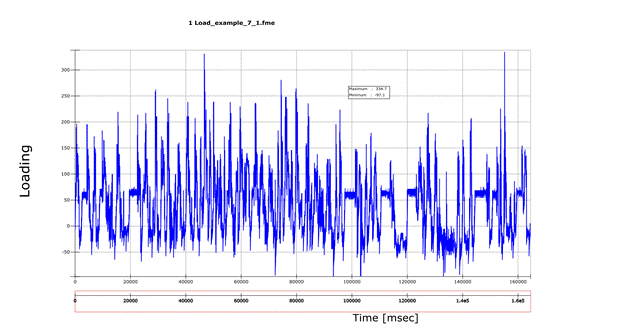
The loading was got from measurement on a test drive. winLIFE makes a rainflow count of the loading and the result is shown in the next figure.

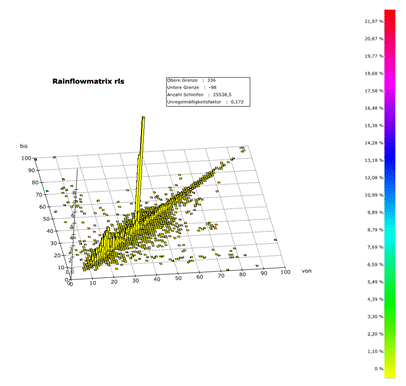
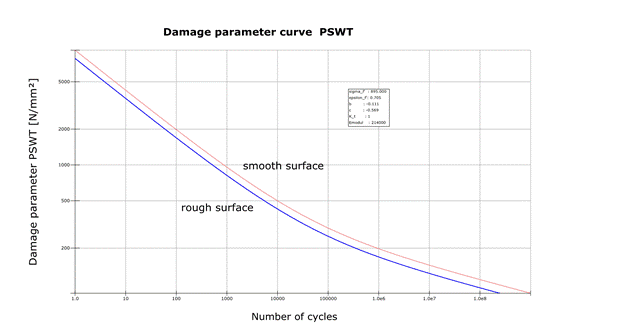
The Material data for fatigue analysis are the cyclic properties (see figure) and the damage parameter life curve (see figure)
 

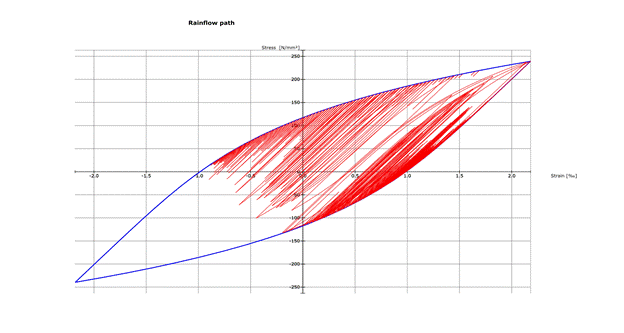
From the rainflow count and the cyclic properties the stress-strain-path is calculated (see figure). Based on the counting and the damage parameter life curve (see figure) a damage sum is calculated for each node of the structure. The results are shown as a map on the structure.

Beside the Local Strain Approach shown here, it is possible to use stress based methods using S-N curves.  As well as the local concept, a stress based concept can also be used for calculation. Here S-N curves can be used based on stresses.

The results of a fatigue life calculation, the damage sum, damage equivalent amplitude. The number of load cycles until failure is available in an Export-File where the FE-Program can access them and show as in the diagram below. For FEMAP an interface is delivered which is automatically installed onto the FEMAP user desktop. 

Without FEA

If no FEA is used the calculation is done only for one point – typically the notch. The information about the geometry and the relation between stress and load now must come from the user. This means he has to enter the notch factor, stress gradient, surface, etc. A fatigue life calculation without FEA can be carried out by the two classic methods - Nominal Stress Method and Local Strain Approach.

With the Nominal Stress Method, various hypotheses can be used to consider the fatigue limit (original, modified according to Haibach, elementary, Liu and Zenner). The following figure shows these possible hypotheses.

If the calculation is done according to the Local Strain Approach, this is done similarly to the procedure using FEA.

Addition of different calculation results

Assume you are developing a car which runs on different road types. You have measurements of each road and fatigue calculations for each road for the measured length. Customers use on the road types will be different in length from that which you have measured. You can now transform the fatigue results from your measured road length to the other length of customers use and you can add the damage sum for the total length of all road types. By adding a weight factor, winLIFE adds together the results of different calculations for each node.

Superposition und Extrapolation

Fatigue Life Calculations are generally carried out for a specified loading. The following test scenario of a test drive with a test vehicle on various types of road surface is an example. Usually there is only one measurement for each part of the route so that the results of the measured journey have to be extrapolated for the required time or route and added together for all parts of the route.

A factor can be calculated from the target and actual values. The results of the test route then have to be multiplied by this factor.  This process is called extrapolation. The user can calculate and set the factor or he can enter the target and actual values and the program will calculate the factor automatically.

The adding together of the results of the individual parts of the route is called superposition.

Table: Data of a test journey with target and actual values and the factor calculated for the extrapolation.

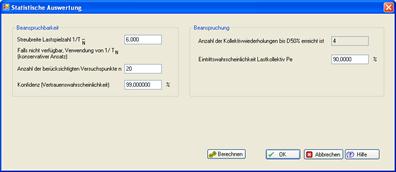
Statistical Analysis

The entry mask shown below enables you to ascertain the statistical reliability. The results from the fatigue life calculation previously carried out and the data from the S-N curve used are taken over. 

Data Handling and Correction

If measured data is used in many cases a data correction is needed. A lot of faults occur and in the first step the user has to check the data. winLIFE enables to check and correct the data simply in an interactive manner.

You can modify load histories and load spectra in the following way:

• find and remove Spikes
• select data and multiplying, adding or overwriting them

Additionally you can modify the number of cycles in a rainflow matrix. This helps to check the results too.

Presenting and analysing the results

All common graphics in result presenting are available, such as:

• Rainflow-Matrix
• Range Mean Pair Count
• Level Crossings
• S-N-Curve together with the load spectrum and percentage damage
• Haigh-diagram including the loads as points 
• Protocol file including the results for each node

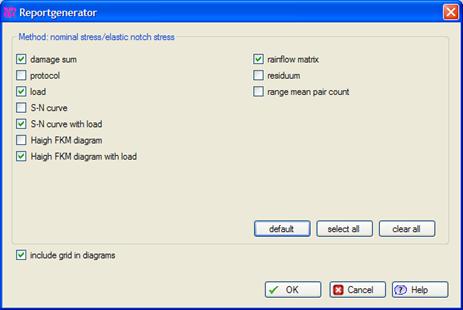
Report Generator

The report generator enables the user to print without individual steps such as opening the graphics. The report generator makes it easier to document a project using only a few work steps. For each method an individual collection of graphics can be selected as shown in the following mask for the Nominal Stress Method. Only one mouse click is needed to create a printout or a PDF-file.

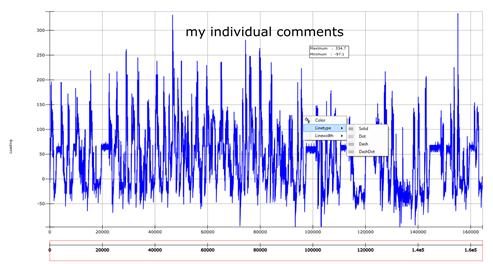
Individual Scaling and designing of Graphics

For each diagram special settings of colour and line type are possible. Clicking on the object shows a window with the properties which can be changed. An example of an individual layout shows the next picture. For each graphic you can select the
Font size

• Line colour
• Line type
• range of axis

 
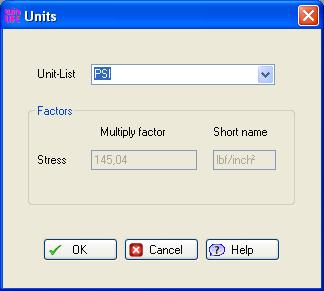
The unit for stresses can be defined in different ways. The internal calculation in winLIFE is done in N/mm2. If another unit for the stress is wished then you can select from the unit-list. Mostly PSI is used and therefore it is prepared.

If you want to define your own unit for stress you can create it by entering the name of the unit and the multiply factor. The other sizes used in winLIFE have the following standard units which cannot be changed. 

strain                                      [‰]

RPM                                       [1/min]